Restarting your sales after a coronavirus lockdown
As I write this, a novel strain of coronavirus (colloquially known as the rona) has a global lockdown. Unemployment rates are skyrocketing, the stock market has dropped substantially, but not nearly as much as consumer sentiment. Millions of businesses around the world, from small businesses like nail salons to tech giants like Airbnb are now facing the same problem: no revenues. At this point, we can only guess how long lockdowns will last. But there are encouraging signs that governments have decided to open. Austria plans to be open in May. For cash strapped businesses, it is essential to get back into action as soon as possible.
In this post, I will show how you can predict who would have purchased from your business, had the lockdowns not happened.
Once the lockdown is over, they are the customers you want to reach out to first. Of course, caveats apply: this does not apply to all business types and the world may not be the same after the virus as it was prior to the virus.
Buy till you die
According to Wikipedia:
The Buy Till You Die (BTYD) class of statistical models are designed to capture the behavioral characteristics of non-contractual customers, or when the company is not able to directly observe when a customer stops being a customer of a brand. The goal is typically to model and forecast customer lifetime value.
BTYD models all jointly model two processes: a repeat purchase process, that explains how frequently customers make purchases while they are still “alive”; and a dropout process, which models how likely a customer is to churn in any given time period.
In other words, the aim of the model is:
- estimate how frequently the customer will purchase
- estimate when the customer will stop purchasing (die)
An advantage of BTYD models is that they only require information on the purchase history of customers. For example:
| Customer ID | Date | Purchase Type | USD Value |
|---|---|---|---|
| 1 | 2020-01-01 | New Widget | 15 |
| 2 | 2020-01-01 | New Widget | 20 |
| 1 | 2020-01-10 | Used Widget | 5 |
Using this information we can compute for each customer:
- The number of repeat transactions per customer (frequency)
- The time of the last recorded transaction (recency)
- The date of the first transaction
- The duration of time between the first transaction and the end of the calibration period
This information is sufficient to fit most BTYD models to estimate orders. Some models can also incorporate:
- Total sales in USD
- The sum over logarithmic intertransaction times (to incorporate purchase regularity into the model)
- Any other customer level covariate (e.g. is the customer a student?)
Markov Chain Monte Carlo Methods
In this case, our primary concern is not to estimate the customer lifetime value, or to figure our which one of our customers is “dead”, but rather to figure out which customer would have purchased from us had the lockdown not happened.
This is where Markov Chain Monte Carlo methods come in. According to Wikipedia:
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution.
MCMC methods make it (relatively) simple to estimate probabilities using that would be otherwise hard (or impossible) to compute.
In our case the probability distribution we are interested in is not P(Alive), nor the distribubtion of orders a customer will make over a given timeframe (the length of the lockdown), but rather the probability that a customer will make at least one purchase over the length of the lockdown.
Example: implementing the model
To implement the model we use the BTYD plus package in R which contains multiple BTYD models. In our case we will use the Abe (2009) model, which allows for predictors to be included.
For this example we’ll use a data set which consists of purchases made by customers of CDNOW in the late 1990s. CDNOW was a billion dollar tech company during the dotcom bubble, which was eventually absorbed by Amazon.
After importing the data and some pre-processing (detailed in the link above), we make the assumption that the pandemic induced lockdowns lasts for two months (from April 1998 to June 1998).
cdnowCbs <- elog2cbs(cdnowElog,
T.cal = "1998-04-30", T.tot = "1998-06-30")
Afterwards, we end up with a dataframe that includes the following columns:
| cust | x | t.x | sales | first | T.cal | T.star | x.star | sales.star | first.sales |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 49.285714 | 100.50 | 1997-01-01 | 69.14286 | 8.714286 | 0 | 0 | 0.02933 |
| 18 | 0 | 0.000000 | 14.96 | 1997-01-04 | 68.71429 | 8.714286 | 0 | 0 | 0.01496 |
| 21 | 1 | 1.714286 | 75.11 | 1997-01-01 | 69.14286 | 8.714286 | 0 | 0 | 0.06334 |
This includes the customer id (cust), the number of repeat transactions (x), the total sales of the customer (sales), the date of the first transaction (first), the duration of time between the first transaction and the end of the calibration period (T.cal).
In our case, we have the data for the period between 1998-04-30 and 1998-06-30, so we also know the actual observed orders in that period (x.star) and value of these sales (sales.star).
In addition, we also included the (scaled) value of the first purchase as a covariate. Now, it is time to run the model.
# draws model parameters using the MCMC methods
draws.m2 <- abe.mcmc.DrawParameters(cdnowCbs, covariates = c("first.sales"),
mcmc = 7500, burnin = 2500)
# using the drawn parameters estimates how many orders the each customer will make
draws_xstar <- mcmc.DrawFutureTransactions(cdnowCbs,draws.m2)
# calculates P(Active) for each customer using the distribution of orders
cdnowCbs$pActive <- mcmc.PActive(draws_xstar)
First, we have to check that the MCMC model has converged. Basically, we want to make sure that the parameters estimated by the MCMC model aren’t complete nonsense.
There are multiple ways of doing this, which we will not go into, but on a superficial level it looks that the model has convergence is okayish. Not great, but not completely useless either.
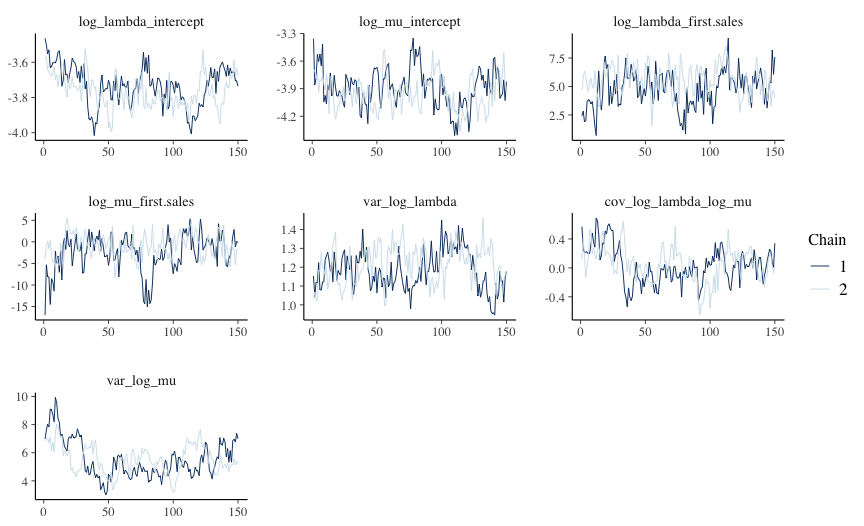
Lets see the results:
| Group P(Active) | Observed P(Active) | Predicted P(Active) | Customers |
|---|---|---|---|
| A: Over 75% | 0.66 | 0.85 | 32 |
| B: Between 50% and 75% | 0.59 | 0.61 | 73 |
| C: Between 25% and 50% | 0.29 | 0.34 | 250 |
| D: Less than 25% | 0.05 | 0.05 | 2002 |
It seems that the model is overestimating the probability of being active at the tail end of customers. We could try to improve the MCMC mixing, or add new predictors.
Nonetheless, these estimates may be sufficient for our purposes.
Summary & Next steps
What you do with this prediction depends to a great extent on your business model, how much each customer is worth, etc. One approach would be to segment your outreach based on the likelihood that they would have purchased.
For example:
- Group A: send them a card/call them.
- Group B: email with new offers.
- Group C: email with a discount code. They need a little bit more of a push to order.
- Group D: email with a larger discount code. These clients were likely lost before the pandemic.